製品紹介

海域施設の耐波設計に適用できる数値波動水路

数値波動水路は、従来の断面2次元造波水路の模型実験に代わり得る手法であり、海域施設の耐波設計への適用を目的に開発され、自由表面や砕波の影響を十分考慮できるものです。
数値波動水路では、水位や流速、加速度や圧力が計算で求められます。波の遡上、リーフによる波の変形、砕波を伴う一様斜面上での波の伝播、ケーソン等の構造物への波力と越波量、反射率など様々な波動現象への適用が試みられています。

• ～数値波動水路の耐波設計への適用に関する研究報告書～沿岸開発技術ライブラリーNo.12参照
• ～数値波動水槽の耐波設計への適用に関する研究会中間報告書～沿岸技術ライブラリーNo.30参照

砕波波形の再現

数値計算の対象となる実験例

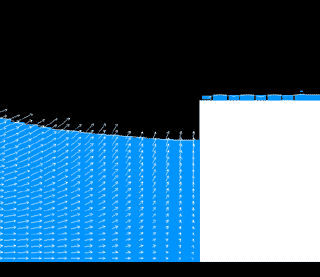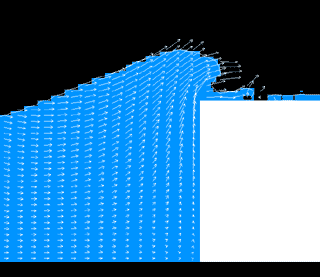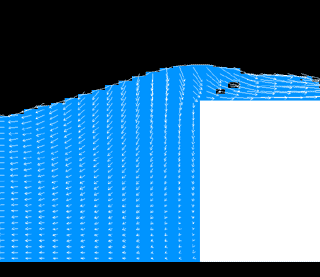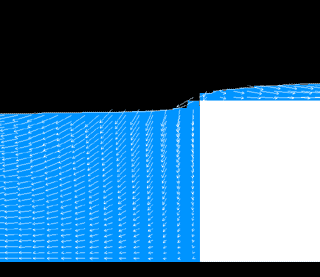
数値計算の例（越波）

機能説明

数値波動水路の機能について

自由表面など移動境界を有する流れ場に対する数値計算法として、高さ関数による方法、マーカー粒子を追跡するMAC（Harlowら、1965）法、Lagrange座標系によるALE法（Hirtら、1972）および境界適合座標法等がよく知られている。 また近年、密度関数法（Miyataら、1988）、Level Set法（Sussmanら、1994）、C-CUP法（Yabe & Wang、1991）並びに粒子法（越塚、1997）などの新しい手法も開発され、我が国の海岸工学の分野でも、多くの成果（藤間ら1984、川崎・岩田1996、榊山ら1997、谷本ら1998、細山田ら1998、渡辺ら1996、陸田ら1998）が挙げられている。 これらの手法の中でも、Hirtら（1981）によるVOF（Volume of Fluid）法は、実用的でしかも複雑な自由表面を取扱ことができる優れた手法といえる。

数値波動水路の数値計算法には、VOF法とSMAC（Simplified Marker and Cell）法を採用し、連立1次方程式の解法に前処理付きBCGSTAB法を用いることで高速・安定な計算を可能としている。 また、設計者が気軽に数値実験を行えるようにするため、数値波動水路のプラットフォームには飛躍的な性能向上をつづけるパーソナルコンピュータを選択した。

特徴

1. 自由表面が多価関数となる複雑な流れを解析対象とする
2. 2次元非圧縮流体のNavier-Stokes(Reynolds)方程式と連続の式を基礎方程式とする
3. 自由表面解析モデルにVOF法を採用する
4. ポーラスモデルを用いて形状近似精度を高める
5. セル単位で任意の位置に構造物や境界条件を設定可能とする
6. 造波モデルとして、造波境界および造波ソースの2つを採用する
7. 造波関数（造波用の流速と水位の計算方法）として、ストークス波等の6種類を採用する
8. 無反射モデルとして、Sommerfeldの放射境界とエネルギー減衰帯の2つを採用する
9. 気泡および水滴の処理として、TimerDoor法を採用する

システム構成の概要

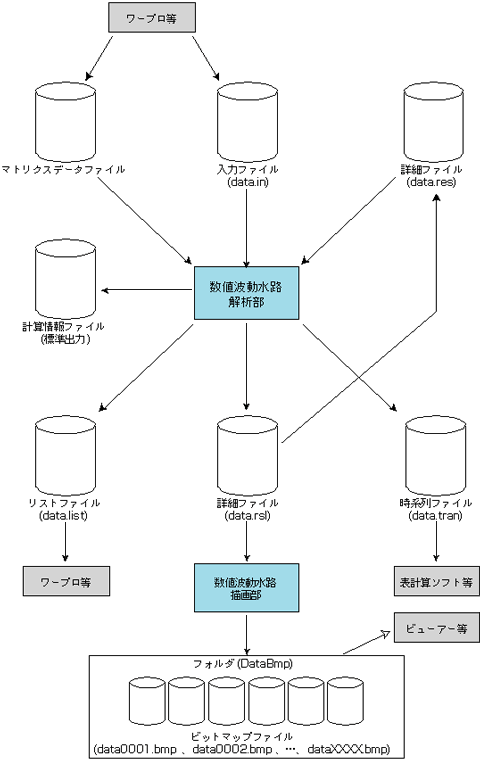
機能一覧

	項目	機能
物理モデル	解析対象	・自由表面が多価関数となる複雑な流れ
	基礎方程式	・2次元非圧縮性粘性流体のNavier-Stokes方程式と連続の式をポーラスモデルに基づいて拡張した式
	座標系	・デカルト座標
	自由表面解析モデル	・Volume of Fluid法（VOF法）
	乱流モデル	・高Re型k-e2方程式モデル
	造波モデル	・造波境界 ・造波ソース （それぞれの造波モデルに以下の造波関数を適用可能）
	造波関数	・ストークス波第5次近似解（定形進行波） ・クノイド波第3次近似解（定形進行波） ・流れ関数法Bによる数値解（定形進行波） ・ピストンタイプ（造波板をモデル化） ・フラップタイプ（造波板をモデル化） ・マトリクスデータ（任意波形）
	無反射モデル	・Sommerfeldの放射境界 ・エネルギー減衰帯
	スカラー量の移流拡散	・多成分のスカラー量の移流拡散計算が可能 （ただし、ユーザルーチンの変更等、ソースプログラムが必須）
	一般の境界条件 （造波境界と放射境界以外）	・セル単位で任意の位置に構造物を設定可能 ・構造物表面の任意の位置に境界条件を設定可能 ・境界条件の種別は入力データで選択可能（スリップ、ノンスリップ、流速指定、対数則、フリー、完全粗面）
数値解法とアルゴリズム	離散化	・スタッガード・メッシュを用いた差分法 ・ポーラスモデルを用いた形状近似
	時間積分	・Euler法 ・Simplified Marker and Cell法（SMAC法）
	移流項（対流項）	・VOF関数F以外の移流項（対流項）は以下のいずれかを選択可能 (1)1次精度風上差分 (2)2次精度中心差分 (3)DONORスキーム（(1)と(2)のハイブリッド形式） (4)QUICKスキーム ・VOF関数Fの移流項はドナー・アクセプタ法で離散化
	表面セルの流速の設定方法	・外挿（流体側の2点の流速から外挿する） ・勾配ゼロ（流体側の流速と同じにする）
	表面の方向の決定方法	・NASA-VOF3Dの方法を採用
	気泡と水滴の処理	・TimerDoor法
	連立1次方程式の解法	・MILU-BCGSTAB法
	時間刻み幅の制御	・入力値固定 ・自動時間刻み幅
描画機能	指定した時刻の場のデータ （描画部を利用）	・流速ベクトル ・各種物理量の等値線 ・等値線による自由表面 ・流体の存在領域の塗り潰し
	時系列データ （表計算ソフトを利用）	・指定個所の初期水面からの水位変動 ・指定個所の計算値、他

境界条件一覧

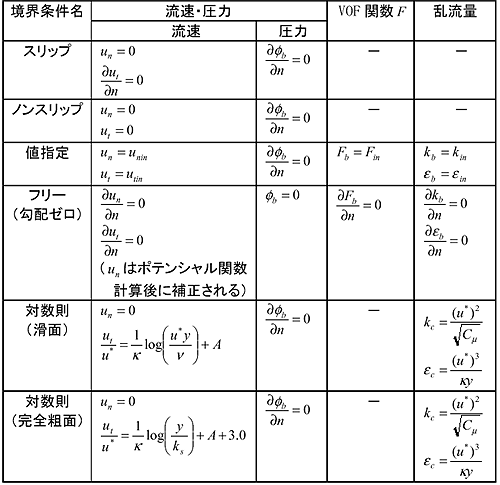
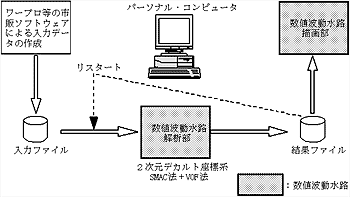
動作環境

沿岸技術ライブラリー No.39
「CADMAS-SURF/3D 数値波動水槽の研究･開発」

海洋構造物の耐波設計を行う際、従来から水理模型実験やそれを基にした設計公式が用いられてきました。水理模型実験を行うには多くの費用と時間が必要であり、設計公式は条件によって精度に問題があります。
そこで、これらに代わる方法として、自由表面の運動をコンピューター上で精度よく追跡できるVOF（Volume of Fluid）法に着目した数値計算法（数値波動水路）の開発を行いました。

その後、「数値波動水槽の耐波設計への適用に関する研究会」を設置し、すでに実用化している2次元の解析理論を基に、3次元構造物へ適用できるように、プログラムの改良、各種構造物への越波・伝達波・波力の計算事例の整備等を行ってきました。

この度、その研究成果を多くの方々へ活用していただくために沿岸技術ライブラリーNo.39として「CADMAS-SURF/3D 数値波動水槽の研究･開発」を発刊することになりました。

本書を参考にしていただくことにより、海洋構造物の設計・研究に携わる方々が、より身近にCADMAS-SURFプログラムを活用していただけるものと確信しています。

お申し込みはこちら

「数値波動水槽路プログラム（CADMAS-SURF/3D）」の公開のご案内

プログラムの提供について

沿岸技術研究センターでは、平成10年に官・学・民からなる「数値波動水路の耐波設計への適用に関する研究会」を設置し、平成13年に初版「CADMAS-SURF」（沿岸技術ライブラリーNo.12）を公開、平成22年には「CADMAS-SURF/3D」（沿岸技術ライブラリーNo.39）を公開し、耐波設計分野において広く活用されてきました。その一方で、実務設計の現場では、CADMAS-SURFを用いた解析において、計算精度や計算の安定性など技術的課題が指摘されていました。

これらを踏まえ、沿岸センターと港湾空港技術研究所は「CADMAS-SURF設計実務研究会」を令和5年度に設置するとともに、実務利用において信頼性の高い数値解析を行うための技術的な運用指針の検討を行ってきました。

このたびCADMAS-SURF/3Dバージョンアップと、その運用指針を示す『実務設計のためのCADMAS-SURF/3D運用指針－精度・安定性を確保する数値波動水槽の活用手引き－』をとりまとめました。

これを機に実務設計等に携わる多くのユーザーに一層活用いただくとともに実務で得られた知見のフィードバックを期待するため、CADMAS-SURF/3D改良版（ver.1.8）を使用許諾付きで無償公開するとともに、技術的運用指針を示す手引きを公開することとなりました。

プログラムおよび手引きの公開によって、多くの研究者や実務設計者がこのプログラムを活用し、全国の港湾施設における耐波設計と整備促進に貢献されることを期待しています。

プログラムのダウンロードは、使用許諾契約書に同意の上ユーザー登録を行ってください。

公開に際してのお願い

1. 使用方法やトラブルに対する問い合わせ対応は致しかねます。
   ・使用方法につきましては、
   ～CADMAS-SURF/3D 数値波動水槽の研究・開発～沿岸技術ライブラリーNo.39を参照してください。
2. 本プログラムを用いて得られた計算結果のすべてについて使用者が責任を持ってください。